Investigating the long-time behavior of the two-dimensional Ising model by leveraging the Java…
Summary
Summary
Novel computational methods are developed to allow for very long time simulations of the two-dimensional Ising model with 10 billion Monte Carlo updates in each simulation. Using these methods, the time-dependent behavior of quenching from random initial states is analyzed to determine the quenching behavior. Simulations are run across a range of parameters, including the lateral size of the grid, l, and the pair interaction strength, J.
In some cases, the simulation trajectory converges to a configuration with a predominantly up spin or a predominantly down spin. There does not appear to be a simple relationship between the parameters of grid lateral size and interaction strength with the behavior of whether or not the simulation converges to a predominant state. In general, smaller lateral grid sizes results are more likely to converge to a single predominant state, which can be explained by the smaller number of spins that need to be aligned. Moderate interaction strengths are found to maximize the fraction of simulated systems that converge to a predominant state with higher interaction strengths leading the system to become arrested in a mixed state configuration.
Background and Introduction
The Ising model is among the simplest models of cooperative behavior in physics and it useful for modeling such phenomena as ferromagnetism. Simpler physics models assume each individual entity operates independently of other entities within the systems. As cooperative phenomena are ubiquitous in nature, it is useful to understand the properties of such a simple model of cooperative interactions. Further, the Ising model has been related to Machine Learning models (see discussion in Quora: How is the Ising model related to machine learning?) and I postulate that it will be increasingly more important as researchers further work to explore and understand the structure of machine learning models.
In the present work, we consider the two-dimension Ising model, which consists of a periodic grid of cells whereby each cell interacts with its four nearest neighbors. Each cell can be in one of two states: up or down. Within this model, it is thermodynamically favorable for neighbors to have aligned spin and we can vary the pair interaction strength through model parameter J.
The following figure shows a small Ising model systems with a periodic grid of lateral size 25 cells.
See the Wikipedia article on the Ising model for more details. Additionally, you can experiment with the Ising model using this in-browser simulation.
In general, there do not exist analytical solutions for the Ising model in two or more dimensions. Instead, numerical simulations are used to sample configurations of the Ising model for subsequent analysis. As in all numerical simulations, there are challenges in propagating the simulated system from an initial chosen configuration — which may be unrepresentative of the configurations of the system at thermal equilibrium — to configurations that are representative. This simulated process is hereby referred to as equilibration because we aim to generate thermodynamically likely configurations of the model.
Due to limitations of computational resources, it’s possible that we will never achieve an equilibrated configuration within the simulated system. Instead, the system will converge towards a local free energy minimum and only explore configurations near that free energy minimum. In such cases, we refer to the systems as being quenched in analogy with physical experiments whereby the system is rapidly brought to a low temperature and therefore the system gets trapped in a local free energy minimum.
To better illustrate this point, let us consider some example configurations of the two-dimensional Ising model. Conventionally, such simulations are initiated from a random initial configuration as shown in the following figure.
Monte Carlo methods are used to propagate the system towards thermal equilibrium, which yields more ordered states with sufficiently high pair interaction.
With a strong enough pair interaction, this can lead the system towards either a fully up spin or a fully down spin configuration for sufficiently small systems.
In contrast, larger simulations will show regions of one spin or another. (Or at least such regions will exist at lower equilibration times with sufficiently high pair interaction strength.)
In large enough systems, it can even be challenging to visually inspect the individual regions as shown in the following lattice of lateral size 5000.
Historically, physicists have studied the properties of such quenched Ising systems to better understand the role of cooperativity in physics. Considering such early work was performed over half a century ago, they had no choice but to investigate quenched systems due to the limitations of computer power.
Now, we have much more powerful computers and software engineering tools and can, therefore, push the methods further to longer equilibration times. In the present work, I leverage the Java Virtual Machine (JVM) to develop a highly efficient simulation of the Ising model and run simulations using cloud resources. The simulations are used to explore the time-dependent equilibration/quenching of Ising model systems with varied size and pair interaction strength. You can find the code at https://github.com/matthagy/ising_java.
Results and Discussion
Using the novel computational methods, a range lateral sizes, l, and pair interaction strengths, J, are simulated using ten billion Monte Carlo updates each. The average spin is computed throughout the simulation and the trajectory of this quantity is analyzed to ascertain the progression of equilibration.
Here’s a video of the simulation of l=500 and J=3kT.
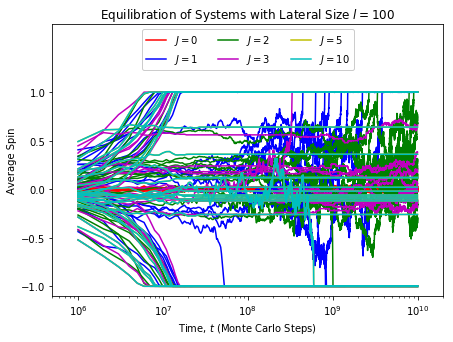
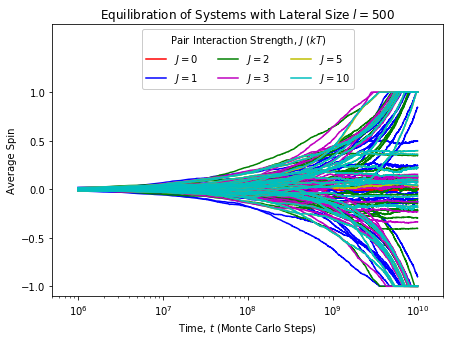
The trajectories of average spin for four different system sizes are shown in the following figures. For each interaction strength, 25 trajectories are collected and shown.
It is noteworthy that many of these trajectories appear to still be converging towards a terminal state, particularly so for the larger lateral size systems.
In inspecting these results, we can see cases where the trajectories terminate in either a fully up spin (1.0) or a fully down spin (-1.0). Other trajectories terminate with the system having a mix of up and down spins. It is noteworthy that the trajectories for l=500 don’t show terminal stabilization, which suggests these systems would tend towards a fully up or down terminal state if simulated for longer.
Next, trajectories are classified as either being in a configuration with a single predominant state or being in a mixed configuration. Specifically, the average spin of the last 100 configurations is computed for each simulation and if the mean spin is greater than 0.95 or less than -0.95, then the system is classified as being in a predominant state. The relationship between pair interaction strength and system lateral size on this behavior is shown in the following figure.
It is noteworthy that a non-monotonic trend is observed with respect to pair interaction strength for smaller lateral sizes of 25 and 50. This suggests that stronger interactions make the system more likely to get stuck in local free energy minima.
Conclusion
This work demonstrates the power of modern computational technologies for performing long-time simulations. Further, the results show that even 10 billion Monte Carlo updates are insufficient for convergence of the quenching process. Nonetheless, the preliminary results show that such simulations can converge to a predominantly up or predominantly down configuration and the conditions under which this occurs is complex with respect to lateral grid size and pair interaction strength.